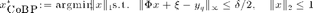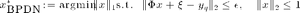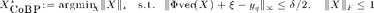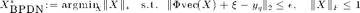Demo for CoBP
The following matlab code provides a demonstration framework for the methods developed in:
A. Moshtaghpour, L. Jacques, V. Cambareri, K. Degraux, C. De Vleesschouwer, "Consistent Basis Pursuit for Signal and Matrix Estimates in Quantized Compressed Sensing"
This script contains two demonstrations: one for K-sparse signal estimation from quantized observations, the other for rank-1 matrix estimation in QCS.
Authors: A. Moshtaghpour, L. Jacques
July, 2015
Contents
Demo 1: K-sparse signal estimation in QCS
As a first demonstration, we propose to reconstruct sparse signals from their quantized compressive observations.
As mentioned in that paper, two methods are tested here for sparse signals:
where 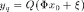 is the quantized compressive measurements of an initial K-sparse signal
is the quantized compressive measurements of an initial K-sparse signal 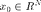 ,
,  is a
is a 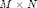 Gaussian Random matrix.
Gaussian Random matrix.
Initializing
addpath('mod_unlocbox'); % Loading toolbox init_unlocbox() % Setting solver parameters param_solver.verbose = 0; % display parameter param_solver.maxit = 60000; % maximum number of iterations param_solver.tol = 1e-6; % tolerance to stop iterating param_solver.gamma = 5e-3; % proximal operator parameter
Conventions
% Size of the signal N = 2048; % Sparsity level K = 16; % Number of measurements M = 64 * K; % Number of bits B = 2; % Quantizer bin width delta = 6/2^(B-1); % BPDN l2 error bound %(see Sec.V: L. Jacques, D. K. Hammond, M. J. Fadili, "Dequantizing compressed sensing") epsilon = delta * sqrt(M+6*sqrt(M))/(2*sqrt(3)); % Uniform midrise quantizer Q = @(x,delta) delta*floor(x/delta) + delta/2;
Generating signals and matrices
% Generating sparse signal with normalized l2 norm idx = randperm(N); x = zeros(N,1); x(idx(1:K)) = randn(K,1); x = x/norm(x); % Generating Gaussian mesurement matrix Phi = randn(M, N); % Generating dithering vector ~U(-delta/2 , delta/2) dithering = -delta/2+delta*rand(M,1);
Acquiring measurements
% Compressive measurements y = Phi * x + dithering; % Quantizing the compressive measurements yq = Q(y,delta);
Solving CoBP and BPDN problems
% BPDN param_solver.init_pt = zeros(N,1); xhat_bpdn = func_BPDN(yq-dithering,Phi,epsilon,param_solver); % CoBP (with a warm start from BPDN solution, works also without) param_solver.init_pt = xhat_bpdn; xhat_cobp = func_CoBP(yq-dithering,Phi,delta,param_solver);
SRE calculation
% CoBP SRE_cobp = 20*log10(norm(x-xhat_cobp)); % BPDN SRE_bpdn = 20*log10(norm(x-xhat_bpdn));
Plotting the results
figure % Ground truth signal subplot(3,1,1) plot(1:N,x,'b-','linewidth',2) title(sprintf('Original %i-sparse signal',K)) xlim([1 N]) ylim([-0.5 0.5]) % CoBP reconstructed signal subplot(3,1,2) plot(1:N,xhat_cobp,'k-','linewidth',2) title(sprintf('CoBP reconstruction, SRE = %2.2g dB',SRE_cobp)) xlim([1 N]) ylim([-0.5 0.5]) % BPDN reconstructed signal subplot(3,1,3) plot(1:N,xhat_bpdn,'r-','linewidth',2) title(sprintf('BPDN reconstruction, SRE = %2.2g dB',SRE_bpdn)) xlim([1 N]) ylim([-0.5 0.5])
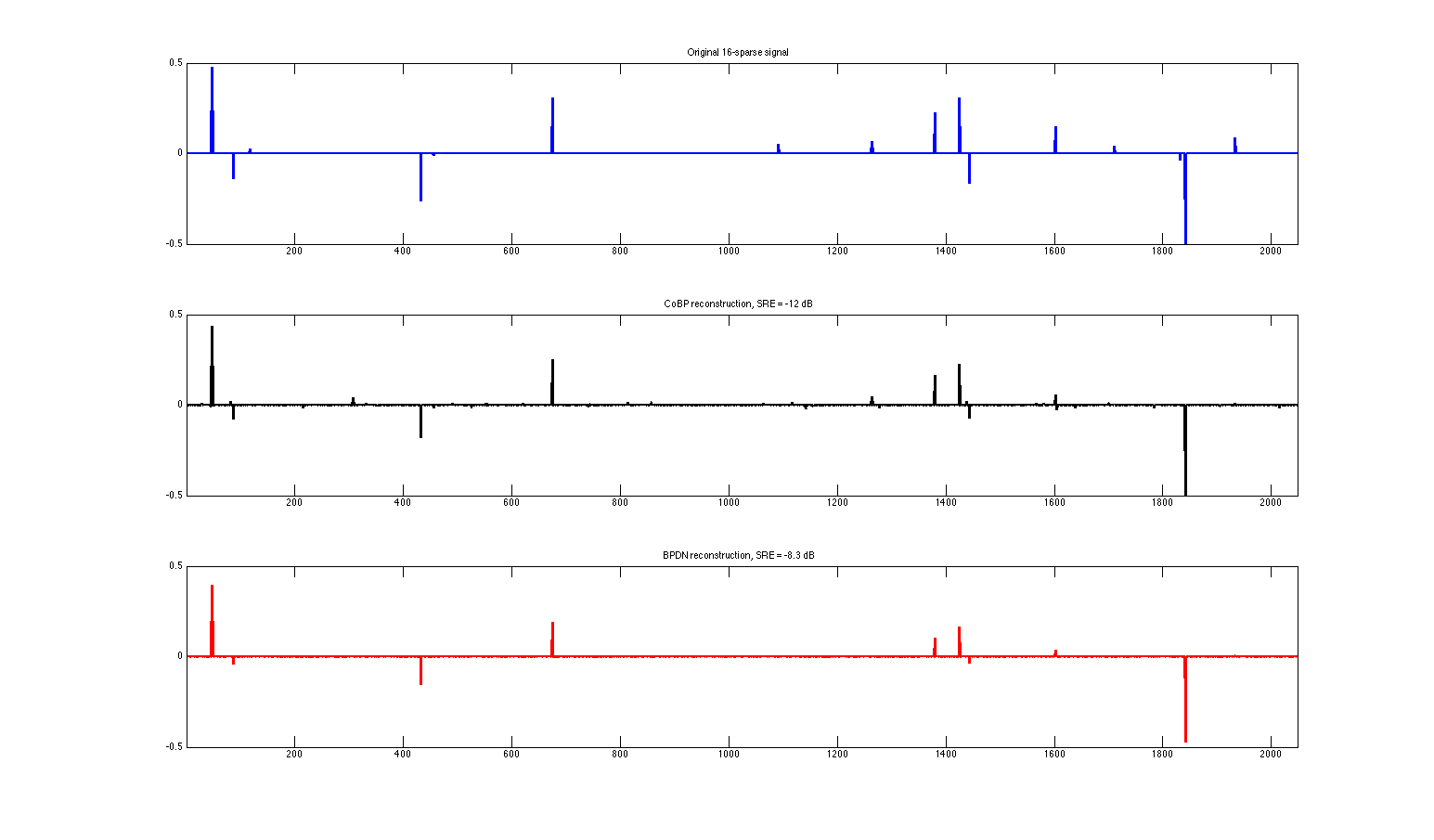
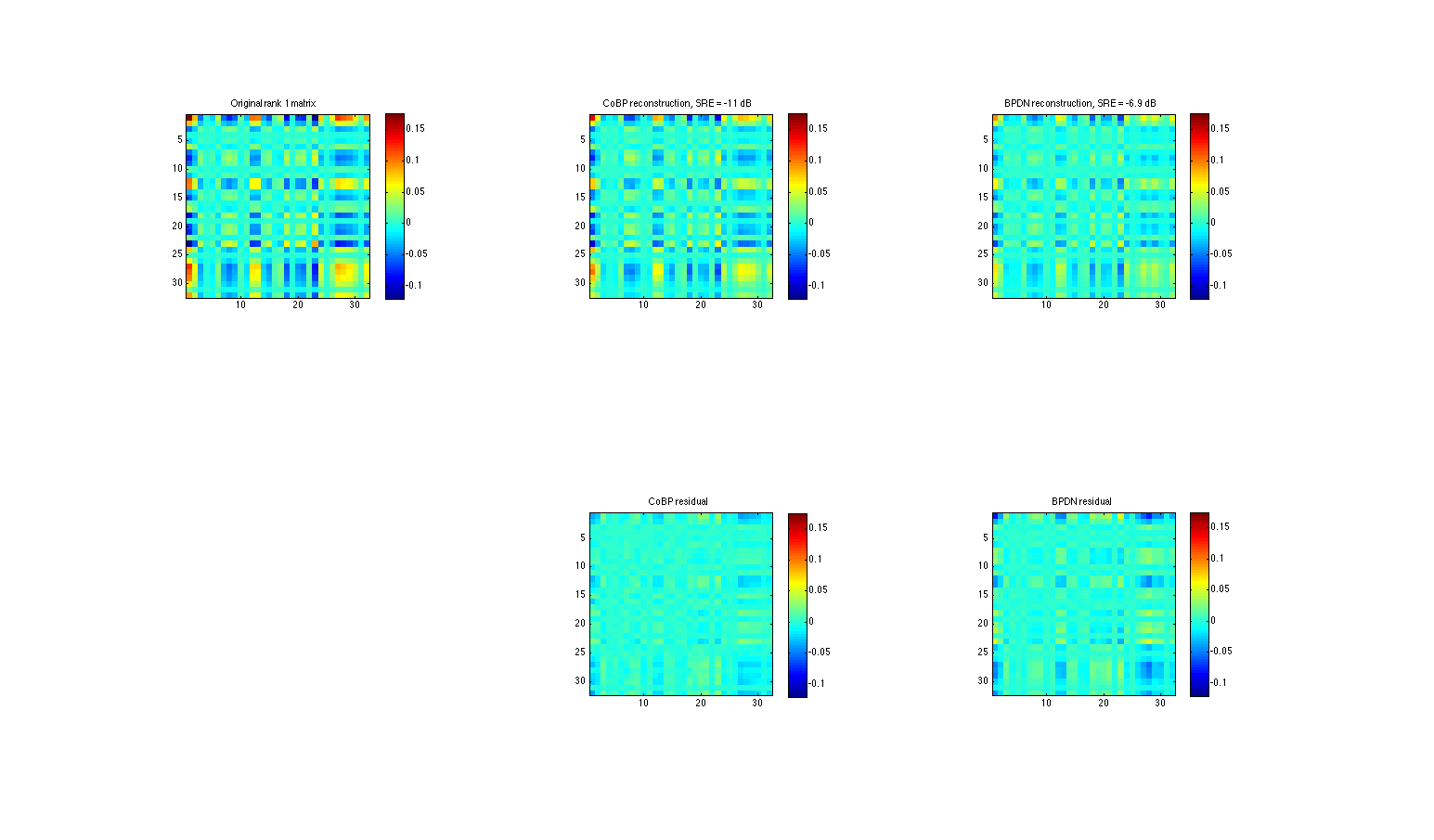
Demo 2: rank-1 matric estimation in QCS
As mentioned in that paper, two methods are tested here for low-rank matrix reconstruction:
where 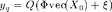 is the quantized compressive measurements of an initial rank-1 matrix
is the quantized compressive measurements of an initial rank-1 matrix 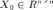 whose vector representation is
whose vector representation is 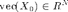 ,
,  is a
is a 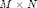 Gaussian Random matrix.
Gaussian Random matrix.
% Setting solver parameters param_solver.verbose = 0; % display parameter param_solver.maxit = 60000; % maximum number of iterations param_solver.tol = 1e-6; % tolerance to stop iterating param_solver.gamma = 5e-3; % proximal operator parameter
Conventions
% Size of the signal N = 1024; n = sqrt(N); % rank of the sensed matrix r = 1; P = 64; % Number of measurements M = 16 * P; % Number of bits B = 2; % Quantizer bin width delta = 6/2^(B-1); % BPDN l2 error bound %(see Sec.V: L. Jacques, D. K. Hammond, M. J. Fadili, "Dequantizing compressed sensing") epsilon = delta * sqrt(M+6*sqrt(M))/(2*sqrt(3)); % Uniform midrise quantizer Q = @(x,delta) delta*floor(x/delta) + delta/2;
Generating signals and matrices
% Generating rank one matrix with normalized Frobenius norm x0 = randn(n,1); X = x0*x0'; X = X/norm(X,'fro'); x = X(:); % Generating Gaussian mesurement matrix Phi = randn(M, N); % Generating dithering vector ~U(-delta/2 , delta/2) dithering = -delta/2+delta*rand(M,1);
Acquiring measurements
% Compressive measurements y = Phi * x + dithering; % Quantizing the compressive measurements yq = Q(y,delta);
Solving CoBP and BPDN problems
% BPDN param_solver.init_pt = zeros(N,1); xhat_bpdn = func_BPDN_matrix_completion(yq-dithering,Phi,epsilon,param_solver); % CoBP (with a warm start from BPDN solution, works also without) param_solver.init_pt = xhat_bpdn; xhat_cobp = func_CoBP_matrix_completion(yq-dithering,Phi,delta,param_solver);
SRE calculation
% CoBP SRE_cobp = 20*log10(norm(x-xhat_cobp)); % BPDN SRE_bpdn = 20*log10(norm(x-xhat_bpdn));
Plotting the results
figure % Ground truth signal subplot(2,3,1) imagesc(reshape(x,[n,n])); caxis([min(x(:)) max(x(:))]) colorbar; axis square; title(sprintf('Original rank %i matrix',r)) % CoBP reconstructed signal subplot(2,3,2) imagesc(reshape(xhat_cobp,[n,n])); caxis([min(x(:)) max(x(:))]) colorbar; axis square; title(sprintf('CoBP reconstruction, SRE = %2.2g dB',SRE_cobp)) % BPDN reconstructed signal subplot(2,3,3) imagesc(reshape(xhat_bpdn,[n,n])); caxis([min(x(:)) max(x(:))]) colorbar; axis square; title(sprintf('BPDN reconstruction, SRE = %2.2g dB',SRE_bpdn)) % CoBP reconstructed signal subplot(2,3,5) imagesc(reshape(xhat_cobp - x,[n,n])); caxis([min(x(:)) max(x(:))]) colorbar; axis square; title('CoBP residual') % BPDN reconstructed signal subplot(2,3,6) imagesc(reshape(xhat_bpdn - x,[n,n])); caxis([min(x(:)) max(x(:))]) colorbar; axis square; title('BPDN residual') % Closing the toolbox close_unlocbox();