Unsupervised compressive learning with spintronics

• Max. student(s): 1
• Advisors: Laurent Jacques and Flavio Abreu Araujo
• Teaching Assistants: Anatole Moureau and Rémi Delogne.

Over the last few years, machine learning—the discipline of automatically fitting mathematical models or rules from data—revolutionized science, engineering, and our society. This revolution is powered by the ever-increasing amounts of digitally recorded data, which are growing at an exponential rate. However, these advances do not come for free, as they incur important computational costs, such as memory requirements, execution time, or energy consumption. To reconcile learning from large-scale data with a reasoned use of computational resources, it seems crucial to research new learning paradigms.

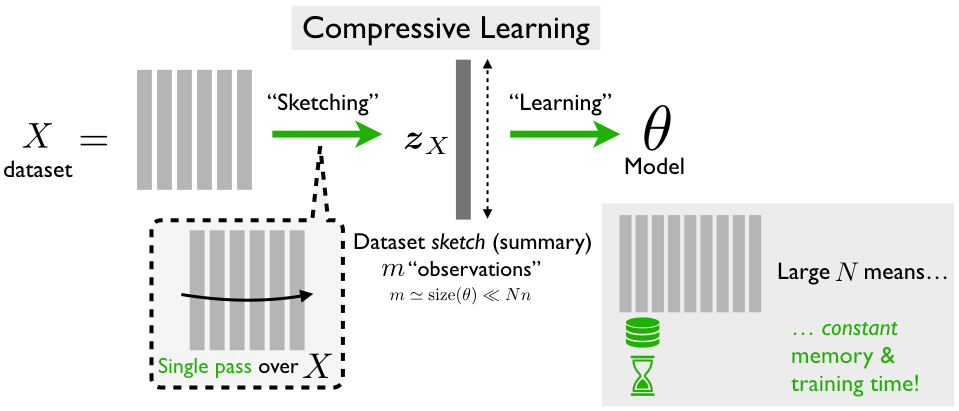
Compressive learning aims at solving large-scale Machine Learning (ML) problems in a resource-efficient manner. In a nutshell (see left figure above), the idea of this method is to first compress a dataset \(X\) in an efficient manner, as lightweight sketch vector \(\boldsymbol z_{X}\). This compression can thus replace a massive dataset of NN high-dimensional elements (made of signals, images, or videos) by a single vector of mm elements with $ m ≪ N$. The desired learning methods are then carried out using only this sketch, instead of the full dataset, which can sometimes save orders of magnitude of computational resources.

That sketch \(\boldsymbol z_{X}\) is a non-linear random feature vector of the data; it uses random oscillating functions (such as sinusoids or imaginary exponential with random frequencies) to probe the statistical content of the dataset. Mathematically, this sketch approximates the characteristic function of the distribution \(\mathcal P\) from which each element of the dataset \(X\) is sampled. For instance, a dataset made of signals or images arranged in several classes (or clusters) can be seen as generated by a mixture of Gaussians. The machine learning algorithm then amounts to finding the right parameters of a parametric distribution for which its characteristic function matches the observed sketch.

One challenge in the sketch computation is the implementation of the oscillating function. While this step is generally implemented digitally, it can slow the computation of a sketch for very large datasets.

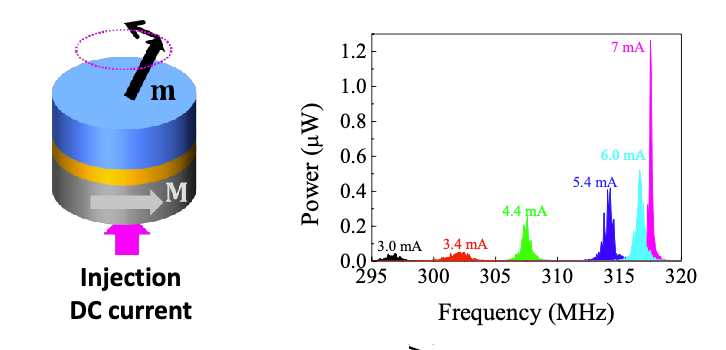
Spintronics devices like spin-torque nano-oscillators, or STNOs (see right figure), can emulate non-linear oscillating functions at the nanoscale. They are composed of two ferromagnetic layers separated by a nonmagnetic material. In these devices, the magnetization dynamics is driven by a spin-polarized current through an effect known as the spin-transfer torque. The amplitude and the frequency of the oscillatory signal has a highly non-linear behavior vs. the input current, and they exhibit an intrinsic memory related to the relaxation of their magnetization. Alternative implementations would require assembling several lumped components and would occupy a much larger area on chip using conventional electronics or photonic technology. STNOs have already been successfully used in machine learning application; recent works show that the non-linearity of their oscillation amplitude can be leveraged to achieve waveform classification for an input signal encoded in the amplitude of the input voltage.

Objective: This master project proposes to study the possibility to compute sketches in the analog domain by leveraging STNOs.

Practically, the master project will consist in the following tasks.

1. Mathematical modeling of the non-linear oscillating function implemented by an STNO. A basic understanding of the physics describing the behavior of STNOs will be have to be gained.
2. Analysis of the specific STNO oscillating function for its use in a compressive learning application. In particular, the student will have to :
   • show how the related STNO sketch captures key statistical properties of a dataset;
   • develop a variant of the compressive K-means algorithm, relying on this sketch, for a non-supervised clustering task.

The master project will be both numerical and theoretical. It will be co-supervised by Prof. Laurent Jacques and Prof. Flavio Abreu Araujo, with the help of Anatole Moureau and Rémi Delogne.

References:

• Gribonval, R., Chatalic, A., Keriven, N., Schellekens, V., Jacques, L., & Schniter, P. (2021). Sketching data sets for large-scale learning: Keeping only what you need. IEEE Signal Processing Magazine, 38(5), 12-36. https://arxiv.org/abs/2008.01839
• Torrejon, Jacob, Riou, Mathieu, Abreu Araujo, Flavio, et al. Neuromorphic computing with nanoscale spintronic oscillators. Nature, 2017, vol. 547, no 7664, p. 428-431. (pdf)
• Keriven, N., Tremblay, N., Traonmilin, Y., & Gribonval, R. (2017, March). Compressive K-means. In 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 6369-6373). IEEE. https://arxiv.org/abs/1610.08738
• Abreu Araujo, Flavio, et al., Role of non-linear data processing on speech recognition task in the framework of reservoir computing, Scientific Reports, 2020, vol. 10, no 328. (pdf)