Posts
Some comments on Noiselets
Update (12/03/25): I have quickly rewritten my original matlab code for computing the forward and inverse Noiselet transforms into Python. This code is available here on GitLab. It is not optimized and can certainly be largely improved.
ROP inception
Here is a new short preprint: “ROP inception: signal estimation with quadratic random sketching”, available here and on arXiv. This is the first work of Rémi Delogne, carried out in collaboration with Vincent Schellekens and me.
There is time for dithering in a quantized world of reduced dimensionality!
I’m glad to announce here a new work made in collaboration with Valerio Cambareri (UCL, Belgium) on quantized embeddings of low-complexity vectors, such as the set of sparse (or compressible) signals in a certain basis/dictionary, the set of low-rank matrices or vectors living in (a union of) subspaces.
Quasi-isometric embeddings of vector sets with quantized sub-Gaussian projections
\(\newcommand{\cl}{\mathcal}\newcommand{\bb}{\mathbb}%\)
Last January, I was honored to be invited in RWTH Aachen University by Holger Rauhut and Sjoerd Dirksen to give a talk on the general topic of quantized compressed sensing.
Testing a Quasi-Isometric Quantized Embedding
It took me a certain time to do it. Here is at least a first attempt to test numerically the validity of some of the results I obtained in “A Quantized Johnson Lindenstrauss Lemma: The Finding of Buffon’s Needle.
When Buffon''s needle problem meets the Johnson-Lindenstrauss Lemma
Last July, I read the biography of Paul Erdős written by Paul Hoffman and entitled “The Man Who Loved Only Numbers”. This is really a wonderful book sprinkled with many anecdotes about the particular life of this great mathematician and about his appealing mathematical obsessions (including prime numbers).
Recovering sparse signals from sparsely corrupted compressed measurements
Last Thursday after an email discussion with Thomas Arildsen, I was thinking again to the nice embedding properties discovered by Y. Plan and R. Vershynin in the context of 1-bit compressed sensing (CS) [1].
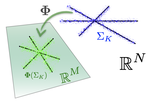
A useless non-RIP Gaussian matrix
Recently, for some unrelated reasons, I discovered that it is actually very easy to generate a Gaussian matrix \(\Phi\) that does not respect the restricted isometry property (RIP) [1]. I recall that such a matrix is RIP if there exists a (restricted isometry) constant \(0<\delta<1\) such that, for any \(K\)-sparse vector \(w \in \mathbb R^N\), \[(1-\delta)\|w\|^2\leq \|\Phi w\|^2 \leq (1+\delta)\|w\|^2.
Tomography of the magnetic fields of the Milky Way?
I have just found this “new” (well 150 years old actually) tomographical method… for measuring the magnetic field of our own galaxy
“New all-sky map shows the magnetic fields of the Milky Way with the highest precision"
New class of RIP matrices?
Wow, almost one year and half without any post here… Shame on me! I’ll try to be more productive with shorter posts now ;-)
I just found this interesting paper about concentration properties of submodular function (very common in “Graph Cut” methods for instance) on arxiv: