Recovering sparse signals from sparsely corrupted compressed measurements

Last Thursday after an email discussion with Thomas Arildsen, I was thinking again to the nice embedding properties discovered by Y. Plan and R. Vershynin in the context of 1-bit compressed sensing (CS) [1].
I was wondering if these could help in showing that a simple variant of basis pursuit denoising using a \(\ell_1\)-fidelity constraint, i.e., a \(\ell_1/\ell_1\) solver, is optimal in recovering sparse signals from sparsely corrupted compressed measurements. After all, one of the key ingredient in 1-bit CS is the \(\rm sign\) operator that is, interestingly, the (sub) gradient of the \(\ell_1\)-norm, and for which many random embedding properties have been recently proved [1,2,4].
The answer seems to be positive when you merge these results with the simplified BPDN optimality proof of E. Candès [3]. I have gathered these developments in a very short technical report on arXiv:
Laurent Jacques, “On the optimality of a L1/L1 solver for sparse signal recovery from sparsely corrupted compressive measurements” (Submitted on 20 Mar 2013)
Abstract: This short note proves the \(\ell_2-\ell_1\) instance optimality of a $ℓ_1ℓ_1$ solver, i.e., a variant of basis pursuit denoising with a \(\ell_1\)-fidelity constraint, when applied to the estimation of sparse (or compressible) signals observed by sparsely corrupted compressive measurements. The approach simply combines two known results due to Y. Plan, R. Vershynin and E. Candès/.
Briefly, in the context where a sparse or compressible signal \(\boldsymbol x \in \mathbb R^N\) is observed by a random Gaussian matrix \(\boldsymbol \Phi \in \mathbb R^{M\times N}\), i.e., with \(\Phi_{ij} \sim_{\rm iid} \mathcal N(0,1)\), according to the noisy sensing model
\[\boldsymbol y = \boldsymbol \Phi \boldsymbol x + \boldsymbol n, \qquad (1),\]
where \(\boldsymbol n\) is a “sparse” noise with bounded \(\ell_1\)-norm \(\|\boldsymbol n\|_1 \leq \epsilon\) (\(\epsilon >0\)), the main point of this note is to show that the \(\ell_1/\ell_1\) program
\[\boldsymbol x^* = {\rm arg min}_{\boldsymbol u} \|\boldsymbol u\|_1 \ {\rm s.t.}\ \| \boldsymbol y - \boldsymbol \Phi \boldsymbol u\|_1\qquad ({\rm BPDN}-\ell_1)\]
provides, under certain conditions, a bounded reconstruction error (aka \(\ell_2-\ell_1\)- instance optimal):

Noticeably, the two conditions (2) and (3) are not unrealistic, I mean, they are not worst than assuming the common restricted isometry property ;-). Indeed, thanks to [1,2], we can show that they hold for random Gaussian matrices as soon as \(M = O(\delta^{-6} K \log N/K)\):
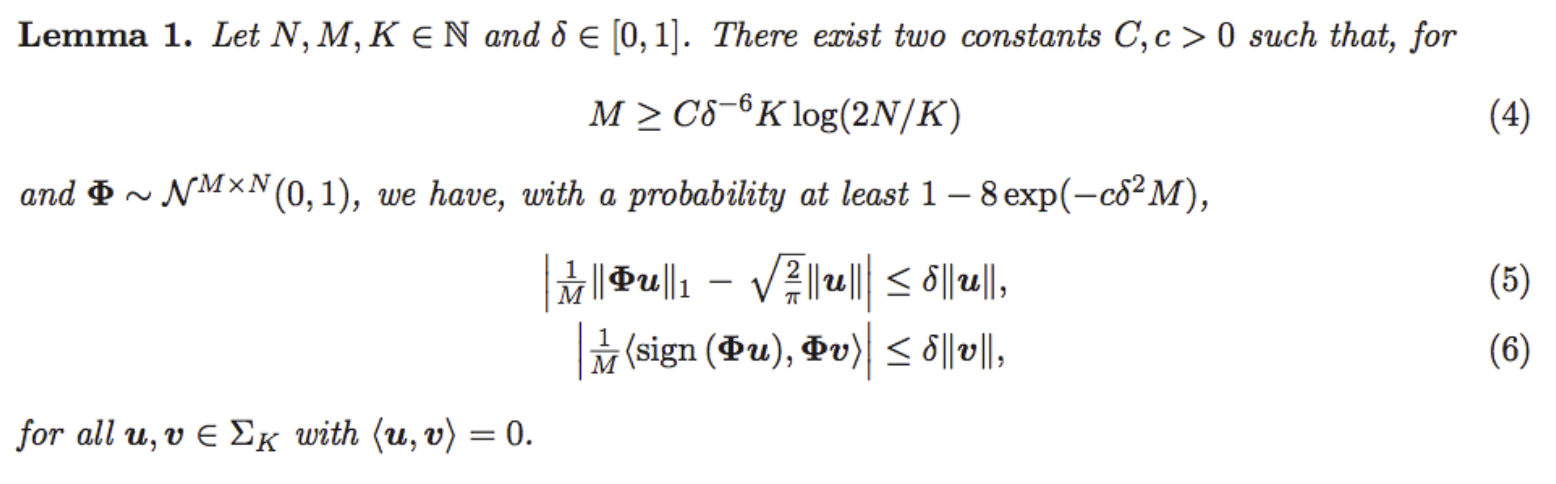
Ass explained in the note, it seems also that the dependency in \(\delta^{-6}\) can be improved to \(\delta^{-2}\) for having (5). The question of proving the same dependence for (6) is open. You’ll find more details (and proofs) in the note.
Comments are of course welcome ;-)
References:
- [1] Y. Plan and R. Vershynin, “Robust 1-bit compressed sensing and sparse logistic regression: A convex programming approach,” IEEE Transactions on Information Theory, to appear., 2012.
- [2] Y. Plan and R. Vershynin, “Dimension reduction by random hyperplane tessellations,” arXiv preprint arXiv:1111.4452, 2011.
- [3] E. Candès, “The restricted isometry property and its implications for compressed sensing,” Compte Rendus de l’Academie des Sciences, Paris, Serie I, vol. 346, pp. 589–592, 2008.
- [4] L. Jacques, J. N. Laska, P. T. Boufounos, and R. G. Baraniuk, “Robust 1-Bit Compressive Sensing via Binary Stable Embeddings of Sparse Vectors” IEEE Transactions on Information Theory, in press.
Image credit: An example of sparse noise that can plague images, the salt-and-pepper noise. Source Wikipedia.