Herglotz-NET: Implicit Neural Representation of Spherical Data with Harmonic Positional Encoding
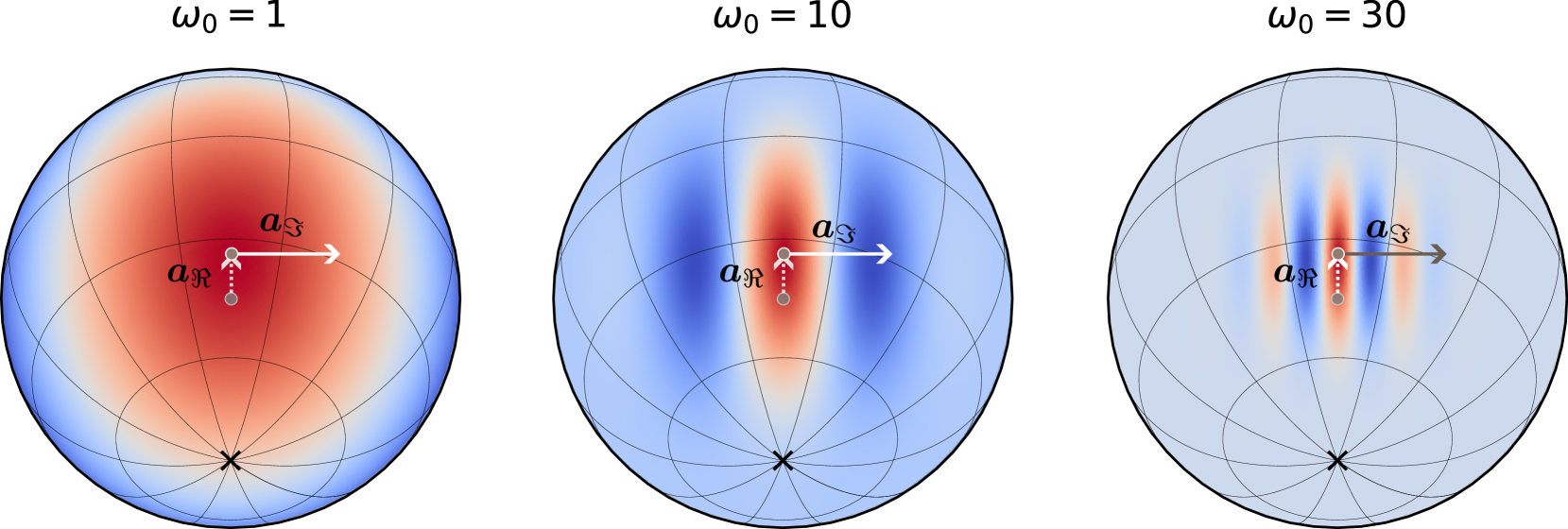
Abstract: Representing and processing data in spherical domains presents unique challenges, primarily due to the curvature of the domain, which complicates the application of classical Euclidean techniques. Implicit neural representations (INRs) have emerged as a promising alternative for high-fidelity data representation; however, to effectively handle spherical domains, these methods must be adapted to the inherent geometry of the sphere to maintain both accuracy and stability. In this context, we propose Herglotz-NET (HNET), a novel INR architecture that employs a harmonic positional encoding based on complex Herglotz mappings. This encoding yields a well-posed representation on the sphere with interpretable and robust spectral properties. Moreover, we present a unified expressivity analysis showing that any spherical-based INR satisfying a mild condition exhibits a predictable spectral expansion that scales with network depth. Our results establish HNET as a scalable and flexible framework for accurate modeling of spherical data.