Fast computation schemes for rank-one projections: application to interferometric imaging

• Max. student(s): 1
• Advisor: Laurent Jacques
• Teaching Assistant: Olivier Leblanc

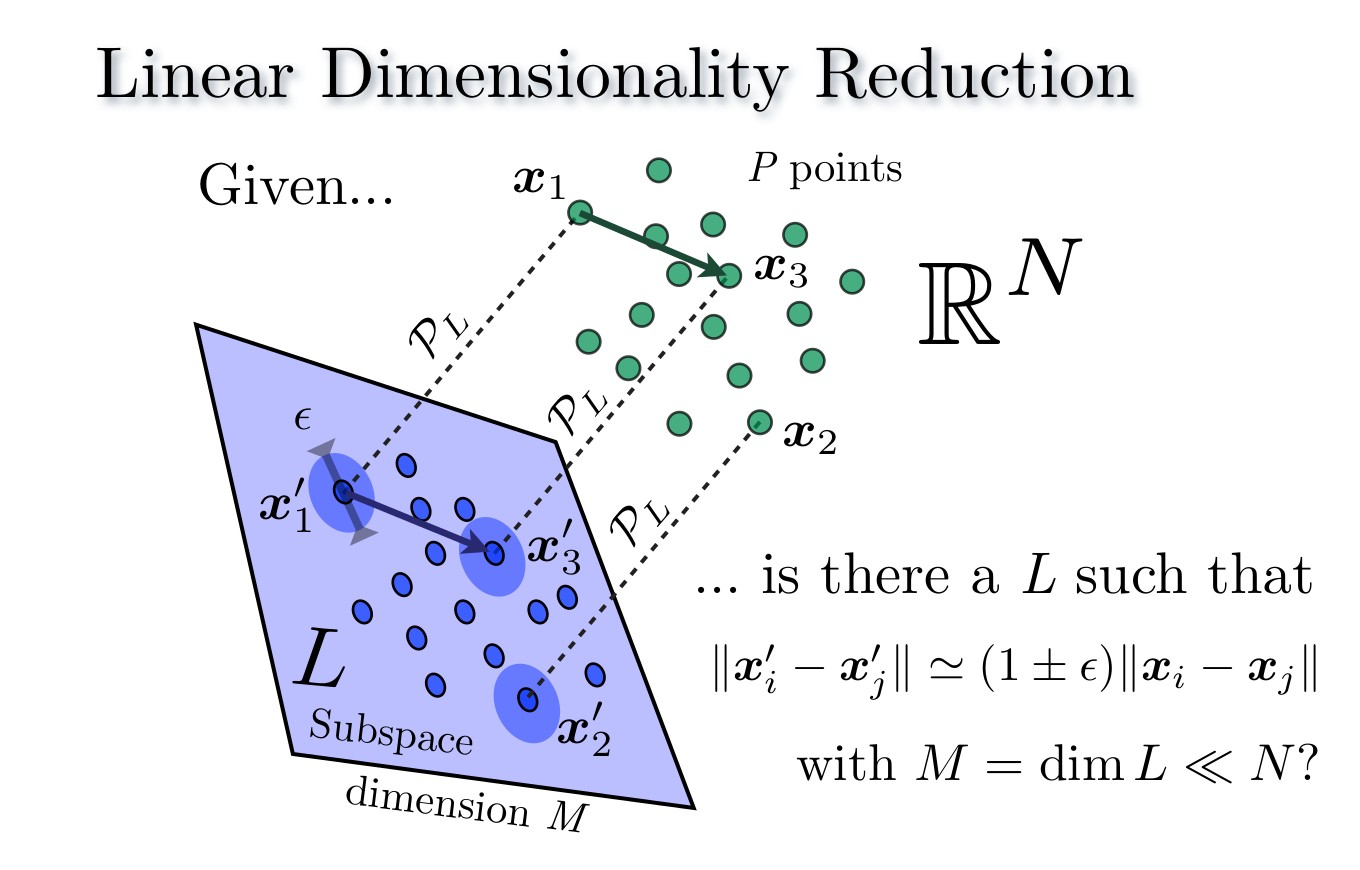
Randomly projecting high-dimensional data to a lower-dimensional domain is at the heart of numerous applications in applied mathematics, data science, big data mining, and signal processing. This data-agnostic compression technique allows for fast computations of a data sketch-a compact summary of the projected data-that still encodes crucial information about the uncompressed data. For instance, as proved by the celebrated Johnson-Lindenstrauss (JL) lemma [1] (see left figure), one can preserve after projection (and up to a controlled distortion) all pairwise distances between dataset elements.

Mathematically, given a dataset \(\left\{x_i\right\}_{i=1}^N \subset \mathbb{R}^n\) of \(N\) data elements in \(\mathbb{R}^n\), a typical random projection consider \(m\) random vectors \(\left\{\varphi_j\right\}_{j=1}^m \subset \mathbb{R}^n\), for instance random Gaussian vectors, and project each vector of the dataset onto these random vectors. We thus create a new dataset \(\left\{x_i’\right\}_{i=1}^N \subset \mathbb{R}^m\) \[ x_i’=\Phi x_i, \quad \text { with } \Phi=\left(\varphi_1, \cdots, \varphi_m\right)^{\top} \] Interestingly, only \(m=O(\log N)\) measurements are necessary to preserve pairwise distance, that is to get \(\left\|x_i’-x_k’\right\| \approx\left\|x_i-x_k\right\|\), thus possibly a huge compression factor for highdimensional datasets. While the first random projection techniques had high computational complexity-for instance, for JL projection, \(\Phi\) being dense, multiplying it with a vector amounts to \(O(m n)\)

More recently, random projections of matrices have also been developed. This is an interesting tool to, for instance, process or filter high-dimensional covariance matrices and hence track potential changes in a stream of data [4]. One of such techniques is the rank-one projection method, or ROP \([3,4]\). Given a \(n \times n\) symmetric matrix \(X \in \mathbb{R}^{n \times n}\), the rank-one projections of this matrix are obtained from: \[ X \in \mathbb{R}^{n \times n} \rightarrow z \in \mathbb{R}^m, \quad \text { with } z_i:=\varphi_i^{\top} X \varphi_i \] with \(m\) random vectors \(\left\{\varphi_j\right\}_{j=1}^m \subset \mathbb{R}^n\). In this context, one can show that one need only \(m=O(\log N)\) to preserve the pairwise distances of a dataset of \(N\) matrices. Moreover, if the dataset is composed only of rank \(r\) matrices, only \(m=O(r n)\) projections are then required, independently of \(N\).

While the memory footprint of the ROP method is relatively low compared to other techniques (only \(m\) vectors of dimension \(n\) must be stored in memory), the computational complexity of the whole projection is, however, of \(O\left(m n^2\right)\) operations. This is quite heavy for high-dimensional matrices.

This master project aims at boosting the computational complexity of the ROP by building the random vectors \(\varphi_i\) as the modulation of a random waveform with sinusoids of varying frequencies, that is, from elements picked a discrete Fourier basis. Practically, this means that we modulate each \(\varphi_i\) to get the random vectors \(\varphi_{i, k}\) such that \[ \varphi_i \rightarrow \varphi_{i, k}=\varphi_i \odot f_k, \quad \text { with }\left(f_k\right)_j=\frac{1}{\sqrt{n}} \exp \left(2 \pi i \frac{j k}{n}\right) \] with \(\odot\) being the pointwise multiplication, and \(f_k\) the \(k\)-th element of the discrete Fourier basis \(F=\left(f_1, \cdots, f_n\right)\).

It is expected, but not yet proved, that a computational complexity of \(O(m n \log n)\) operations is achievable to compute \(m\) ROPs. Accordingly, the objectives of this master project will be to:

• determine a fast scheme to compute ROP of symmetric matrices;
• show numerically (and possibly theoretically) that the boosted ROP scheme also preserves the pairwise distances of a set of matrices;
• show that the boosted ROP can be applied to specific machine learning algorithms (such as SVM or kNN) to reduce their computational complexity while approximately preserving their performances.

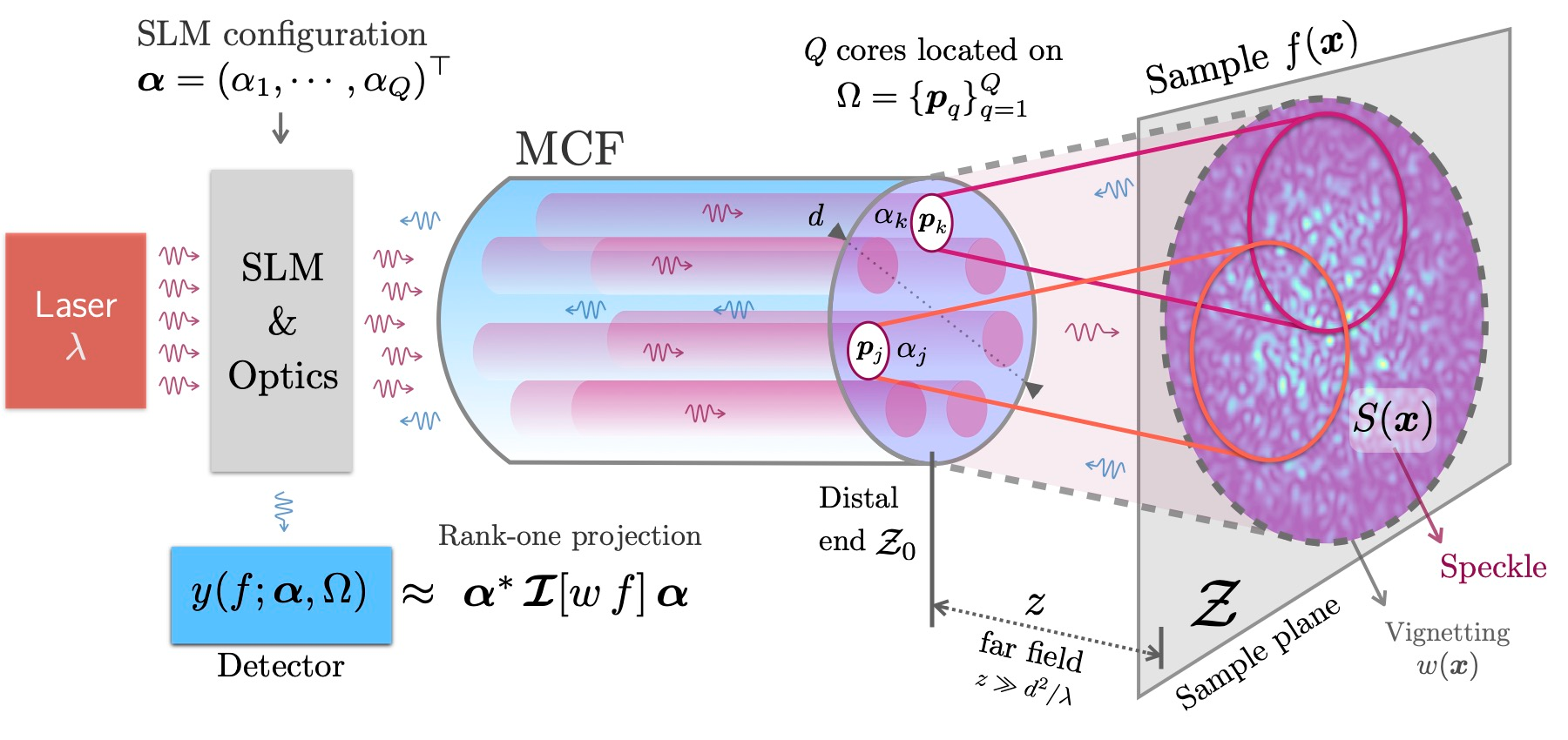
Of related interest for this project, is also the use of boosted ROP for the measurement of interferometric matrices, a special type of matrix encoding information about an image of interest in the context of compressive lensless imaging with multicore optical fibers [5] (see right figure). The results achieved by this master project could be directly applied to this application in collaboration with Hervé Rigneault (Institut Fresnel, France).

For more information about this master project, the interested student can contact Prof. Laurent Jacques or Olivier Leblanc. The regular supervision of this project will be ensured by these two persons.

References:

[1] William B. Johnson and Joram Lindenstrauss. Extensions of Lipschitz mappings into a Hilbert space. Contemporary Mathematics, 26:189–206, 1984.

[2] Ailon, N., & Chazelle, B. (2009). The fast Johnson–Lindenstrauss transform and approximate nearest neighbors. SIAM Journal on computing, 39(1), 302-322.

[3] Cai, T. T., & Zhang, A. (2015). ROP: Matrix recovery via rank-one projections. The Annals of Statistics, 43(1), 102-138. (https://arxiv.org/abs/1310.5791) + Video

[4] Chen, Y., Chi, Y., & Goldsmith, A. J. (2015). Exact and stable covariance estimation from quadratic sampling via convex programming. IEEE Transactions on Information Theory, 61(7), 4034-4059. https://arxiv.org/abs/1310.0807

[5] Laurent Jacques, Olivier Leblanc, Siddharth Sivankutty, Hervé Rigneault, “Interferometric Lensless Endoscopy: Rank-one Projections of Image Frequencies with Speckle Illuminations”, Special session on “Computational Sampling”, organized by Ayush Bhandari (Imperial College, UK), Asilomar, 2021. (slides) (video)