ROP inception

Here is a new short preprint: “ROP inception: signal estimation with quadratic random sketching”, available here and on arXiv. This is the first work of Rémi Delogne, carried out in collaboration with Vincent Schellekens and me.

In this preprint, we show how we can estimate the square of the similarity of a pattern \(\boldsymbol p \in \mathbb R^{n}\) with a signal \(\boldsymbol x \in \mathbb R^{n}\), that is \((\boldsymbol p^{\top} \boldsymbol x)^{2}\) directly from its quadratic random sketch— equivalent to the rank-one projections, or ROP, of \(\boldsymbol x \boldsymbol x^\top \in \mathbb R^{n \times n}\). This sketching is defined by \[ \boldsymbol x \mapsto {\rm Sk}(\boldsymbol x) := \{(\boldsymbol a_{i}^{\top} \boldsymbol x)^{2}\}_{i=1}^{m} = \{ \langle\boldsymbol a_{i}\boldsymbol a_{i}^{\top},\boldsymbol x\boldsymbol x^{\top}\rangle \}_{i=1}^{m}, \] for a collection of \(m\) random vectors \(\{ \boldsymbol a_{i}\}_{i=1}^{m}\) (we assume them Gaussian).

This operator is considered, for instance, in phase retrieval problems [5], where we only observe the spectral amplitudes of a signal, in the estimation of structured covariance matrices [1,2], or in the recent optical processing units (OPU) [3,4]. Under certain conditions, this sketch allows for some form of dimensionality reduction, or it can embed data in a larger feature space, more amenable to certain machine learning tasks.

Up to a small debiasing of the sketch, we show that to estimate this similarity with the pattern \(\boldsymbol p\), you just need to project the signal sketch \({\rm Sk}(\boldsymbol x)\) onto the “sign” of the pattern sketch, that is \({\rm sign}({\rm Sk}(\boldsymbol p))\), where the sign operator, applied componentwise onto vectors, simply replaces a value by its sign.

You can then approximate from this projection (and with some controlled distortion) the square of this similarity, that is \((\boldsymbol p^{\top} \boldsymbol x)^{2}\), which is just another ROP (or quadratic sketch) of \(\boldsymbol x\); we just did a kind of “ROP inception” in a ROP model ;-)

As we don’t need the ROP adjoint in this similarity estimation, our approach could potentially allow for specific signal processing in the sketched domain of quadratic observations, such as those provided by certain optical setups (e.g., interferometry [5], OPU [3,4]), in a similar way to what was done in compressive sensing (see for instance [6]). Under the hood, this approach relies on some tools of one-bit compressive sensing, such as the sign product embedding [7,8].

In our work, we show experimentally that this estimation enables us to locate a rotating disk in one of the four quadrants of an image using only the image ROPs.

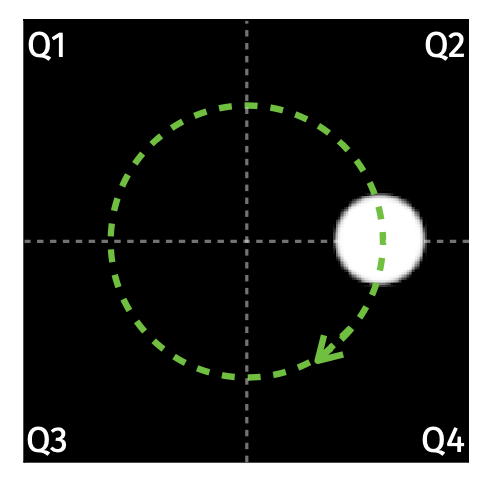
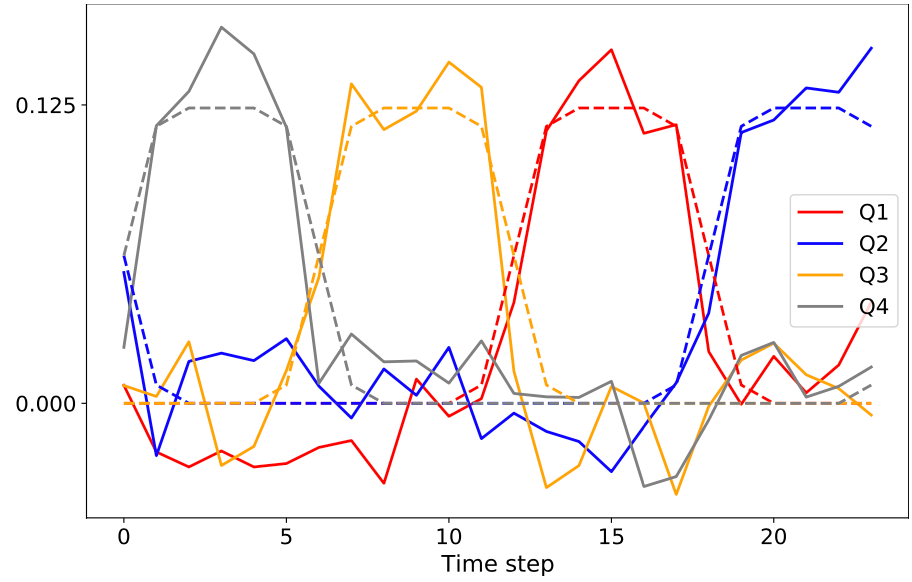
We also demonstrate that we can still classify MNIST handwritten digit images directly in the ROP domain, with testing accuracy comparable to a direct processing of these images.

Moreover, if the classification is directly operated in the sketched domain (by simply computing the classes’ centroid), applying a sign operation to the centroids (and thus assimilating each of these centroids as the quadratic sketch of some representative image) improved the classification accuracy compared to the one achieved in the direct domain, without any sketching (as shown in the last column of this table, see the paper for the convention).

References:

• [1] Y. Chen, Y. Chi, A.J. Goldsmith, Exact and Stable Covariance Estimation From Quadratic Sampling via Convex Programming, IEEE Transactions on Information Theory, vol. 61, no. 7, 2015.
• [2] T. Cai, and A. Zhang., ROP: Matrix Recovery via Rank One Projections, The Annals of Statistics, vol. 43, no. 1, pp. 102-38, 2015.
• [3] A. Saade, F. Caltagirone, I. Carron, L. Daudet, A. Dr ́emeau, S. Gigan, and F. Krzakala, Random projections through multiple optical scattering: Approximating kernels at the speed of light. In IEEE ICASSP 2016 (pp. 6215-6219).
• [4] https://lighton.ai
• [5] E.J. Candès, T. Strohmer, and V. Voroninski, PhaseLift: Exact and Stable Signal Recovery from Magnitude Measurements via Convex Programming.,Comm. Pure Appl. Math., 66: 1241-1274, 2013.
• [6] P.T. Boufounos, M.B. Wakin, R.G. Baraniuk, M.A. Davenport, Signal processing with compressive measurements, IEEE Journal of Selected topics in Signal processing, 4(2), 445-460. 2010.
• [7] L. Jacques, K. Degraux, C. De Vleeschouwer, Quantized Iterative Hard Thresholding: Bridging 1-bit and High-Resolution Quantized Compressed Sensing. Proceedings of International Conference on Sampling Theory and Applications, IEEE 2013, p.105-108, 2013.
• [8] S. Foucart, Flavors of Compressive Sensing. In: Fasshauer, G., Schumaker, L. Approxim- ation Theory XV: San Antonio 2016. AT 2016. Springer Proceedings in Mathematics & Statistics, vol 201, Springer, 2017.