johnson-lindenstrauss
Quasi-isometric embeddings of vector sets with quantized sub-Gaussian projections
Last January, I was honored to be invited in RWTH Aachen University by Holger Rauhut and Sjoerd Dirksen to give a talk on the general topic of quantized compressed sensing. In particular, I decided to focus my presentation on the quasi-isometric embeddings arising in 1-bit compressed sensing, as developed by a few researchers in this field (e.
Quasi-isometric embeddings of vector sets with quantized sub-Gaussian projections
\(\newcommand{\cl}{\mathcal}\newcommand{\bb}{\mathbb}%\)
Last January, I was honored to be invited in RWTH Aachen University by Holger Rauhut and Sjoerd Dirksen to give a talk on the general topic of quantized compressed sensing.
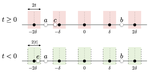
When Buffon's needle problem helps in quantizing the Johnson-Lindenstrauss Lemma
Abstract: In 1733, Georges-Louis Leclerc, Comte de Buffon in France, set the ground of geometric probability theory by defining an enlightening problem: What is the probability that a needle thrown randomly on a ground made of equispaced parallel strips lies on two of them?
Testing a Quasi-Isometric Quantized Embedding
It took me a certain time to do it. Here is at least a first attempt to test numerically the validity of some of the results I obtained in “A Quantized Johnson Lindenstrauss Lemma: The Finding of Buffon’s Needle” (arXiv) I have decided to avoid using the too conventional matlab environment.
When Buffon's needle problem meets the Johnson-Lindenstrauss Lemma
Quasi-isometric embeddings of vector sets with quantized sub-Gaussian projections | Le Petit Chercheur Illustré - Apr 2, 2015
[…] explained in my previous post on quantized embedding and the funny connection with Buffon’s needle problem, I have recently noticed that for finite […]
When Buffon's needle problem meets the Johnson-Lindenstrauss Lemma
[caption id=“attachment_346” align=“alignnone” width=“640”] (left) Picture of [8, page 147] stating the initial formulation of Buffon’s needle problem (Courtesy of E. Kowalski’s blog) (right) Scheme of Buffon’s needle problem.[/caption](This post is related to a paper entitled “A Quantized Johnson Lindenstrauss Lemma: The Finding of Buffon’s Needle” (arxiv, pdf) that I have recently submitted for publication.
When Buffon''s needle problem meets the Johnson-Lindenstrauss Lemma
Last July, I read the biography of Paul Erdős written by Paul Hoffman and entitled “The Man Who Loved Only Numbers”. This is really a wonderful book sprinkled with many anecdotes about the particular life of this great mathematician and about his appealing mathematical obsessions (including prime numbers).