General

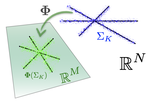
Recently, for some unrelated reasons, I discovered that it is actually very easy to generate a Gaussian matrix \(\Phi\) that does not respect the restricted isometry property (RIP) [1]. I recall that such a matrix is RIP if there exists a (restricted isometry) constant \(0<\delta<1\) such that, for any \(K\)-sparse vector \(w \in \mathbb R^N\), \[(1-\delta)\|w\|^2\leq \|\Phi w\|^2 \leq (1+\delta)\|w\|^2.

Laurent Duval - Dec 5, 2011 16 month is quite short when you compare to cosmic times

I have just found this “new” (well 150 years old actually) tomographical method… for measuring the magnetic field of our own galaxy “New all-sky map shows the magnetic fields of the Milky Way with the highest precision”

I have just found this “new” (well 150 years old actually) tomographical method… for measuring the magnetic field of our own galaxy “New all-sky map shows the magnetic fields of the Milky Way with the highest precision"

Igor Carron - May 3, 2010 Laurent, Do you think that g could be behaving like the quantization function in the 1-bit compressive sensing approach of Petros ? http://www.merl.com/reports/docs/TR2010-014.pdf Cheers, Igor.

Wouaw, almost one year and half without any post here…. Shame on me! I’ll try to be more productive with shorter posts now ;-) I just found this interesting paper about concentration properties of submodular function (very common in “Graph Cut” methods for instance) on arxiv:

Wow, almost one year and half without any post here… Shame on me! I’ll try to be more productive with shorter posts now ;-) I just found this interesting paper about concentration properties of submodular function (very common in “Graph Cut” methods for instance) on arxiv:

I have always been intrigued by the fact that, in Compressed Sensing (CS), beyond Gaussian random matrices, a couple of other unstructured random matrices respecting, with high probability (whp), the Restricted Isometry Property (RIP) look like “quantized” version of the Gaussian case, i.

1000th visit and some Compressed Sensing “humour” - Apr 5, 2012 […] http://yetaspblog.wordpress.com/2008/11/23/1000th-visit-and-some-compressed-sensing-humour/ […] #### [pedrock](http:// "pedrock.opiniatre@gmail.com") - Nov 2, 2008 Merci pour le Blogroll ;) Pedrock #### [jackdurden]( "

As detected by Igor Carron, this blog has reached its 1000th visit ! Well, perhaps it’s 1000th robot visit ;-) Yesterday I found some very funny (math) jokes on Bjørn’s maths blog about “How to catch a lion in the Sahara desert” with some … mathematical tools.