random projections

Quasi-isometric embeddings of vector sets with quantized sub-Gaussian projections

\(\newcommand{\cl}{\mathcal}\newcommand{\bb}{\mathbb}%\) Last January, I was honored to be invited in RWTH Aachen University by Holger Rauhut and Sjoerd Dirksen to give a talk on the general topic of quantized compressed sensing.
Apr 28, 2015 12 min read
Quasi-isometric embeddings of vector sets with quantized sub-Gaussian projections

A Quantized Johnson Lindenstrauss Lemma: The Finding of Buffon's Needle

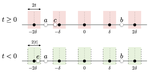
Abstract: In 1733, Georges-Louis Leclerc, Comte de Buffon in France, set the ground of geometric probability theory by defining an enlightening problem: What is the probability that a needle thrown randomly on a ground made of equispaced parallel strips lies on two of them?
2015 IEEE Transactions on Information Theory
DOI DIAL arXiv ipynb Demo

When Buffon's needle problem helps in quantizing the Johnson-Lindenstrauss Lemma

Abstract: In 1733, Georges-Louis Leclerc, Comte de Buffon in France, set the ground of geometric probability theory by defining an enlightening problem: What is the probability that a needle thrown randomly on a ground made of equispaced parallel strips lies on two of them?